【森を見よ】２✕３の呪縛

小学校の算数で「２✕３は２が３個」と習います。つまり

２✕３＝２＋２＋２

ということですね。

「みかんが２つ入っている袋が３つある。みかんは全部でいくつ？」

この問題は２✕３で解くんだよ、と教わります。そのとき、これを３✕２と書くと不正解になる（と記憶しています）。

小学校の高学年だと思うのですが、掛け算の前後を入れ替えても答えは同じになることを習います。これを数学では「交換法則」とか「可換律」といいます。

２✕３＝３✕２

ということですね。これは、箱に入ったまんじゅうの例で説明できます。

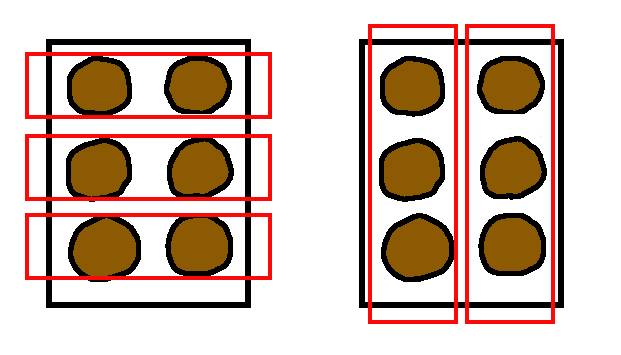
はこには６個のまんじゅうが長方形に並んでいます。左側では、横に２つ並んだまんじゅうのグループが３つあるので「２✕３」。右側では、縦に３つ並んだまんじゅうのグループが２つあるので「３✕２」。どちらもまんじゅうの総数６に等しいので、

２✕３＝３✕２

２と３に限らず、どの掛け算も「箱入りまんじゅう」の縦横の数だと思えば同様に交換法則が成り立つことが分かります。

交換法則が成り立つのだから「２✕３」の意味を２通りのどちらでも良いと見ることができます。

小学校低学年では「２✕３」は上の意味であって、下の意味ではないと教えるのは、児童が無用の混乱をきたさないための教育上の手法です。本当は２通りの意味が含まれると考えるのが正しいです。

中学になって文字式を習うと「 $2x$ 」が出てきます。

のどちらも正しいけれども、通常は「 $x$ が２個」でしょう。

小学校で習った解釈ではなく、小学校で誤りとされた考えが正しいわけです。おそらく、ここで混乱する中学生は少なくないと思います。なぜ「 $x2$ 」じゃなくて「 $2x$ 」なのか？すぐに理解できるようになるとは思いますが・・・

英語で「２✕３」は

です。それぞれ、

に対応するように思いますが、「timesの方は両方の解釈ができる」というネット情報もありました。ネイティブの間でも議論になるようです。

蛇足ですが、

A is three times as big as B.　＝＞　AはBの３倍の大きさである

A is three times bigger than B.　＝＞　「AはBの４倍の大きさである」との解釈も成り立つ

で、前者が曖昧さの残らない表現でよろしい、ということだそうです。

おもこん