マイナスの数の掛け算について書きます。 よくある間違いに、マイナス✕マイナスがマイナスになる、というのがあります。 正しくはプラスになる、と教わるのですが「なぜ?」となってしまうのです。 そう思う理由は、
- プラス✕プラスがプラスになるから、マイナス✕マイナスがマイナスになる
- プラスにマイナスをかけるとマイナス、つまり小さくなる。 だからマイナスにマイナスをかければ余計小さくなるはずだ
などでしょう。
これは掛け算の一部を見て類推しているのです。 もっと掛け算の全体を見なければならないのですね。
負数(マイナスの数)の仕組み
−2は数なんだから、「ー」と「2」を分けてはだめ、「−2」でひとつの数だから。
負数を習うと最初はこう教えられるかもしれませんが、実は「−2」は「ー」と「2」に分けて考えるべきです。
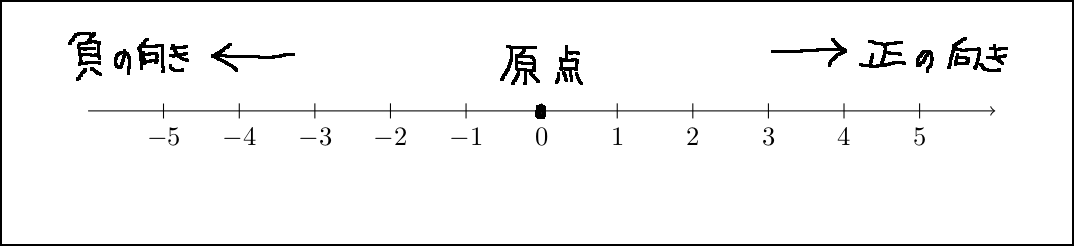
- 「ー」は「+」と逆の向きを表す
- 「2」はプラスとマイナスの中間にある「0」からの距離を表す
実は正の数も同じで「5」と「+5」は同じで、向きが「+」の向き(一般には正の向きという)で0からの距離が「5」です。
「プラス✕プラス」と「マイナス✕プラス」
2✕3は2を3回足すことだから、6になります。
2✕3=2+2+2=6
同じように考えれば、(−2)✕3は−6になります。
(−2)✕3=(−2)+(−2)+(−2)=−6
このように「3をかける」というのは
- 向きを変えず
- 大きさを3倍(0からの距離を3倍)
ですが、「向きを変えず」というのは大事なポイントです。
「プラス✕マイナス」
掛け算は前後を入れ替えても同じになるので、
3✕(−2)=(−2)✕3=−6
ですが、ここから「−2をかける」というのは
- 向きが反対になる(正の数が負の数になる)
- 大きさが2倍(0からの距離が2倍)
ということになります。 ここで、向きが反対になるのは「−2」の「ー」の部分のためです。大きさ2倍は「−2」の「2」の部分が関わっています。
「マイナス✕マイナス」
「−3」をかけると「向きが反対」「おおきさ3倍」ですから、
(−2)✕(−3)=6
- −2は負の向きなので、向きを変えると「正の向き」
- 0からの距離は2の3倍で6
ということですね。 だから、マイナス✕マイナスは(向きが反対になるから)プラスになります。
数学的、形式的な論法
形式的には、マイナスの数はプラスの数の逆元として導入していくことになるので、
(−3)+3=0
負数でも分配法則が成り立てば
(−2)✕{(−3)+3}=(−2)✕0 (−2)✕(−3)+(−2)✕3=0 (−2)✕(−3)+(−6)=0 (−2)✕(−3)=6
このようにマイナス✕マイナスがプラスにならなければならない。 そうでなければ、分配法則は負の数では使えなくなってしまう、ということです。
発展編=>虚数
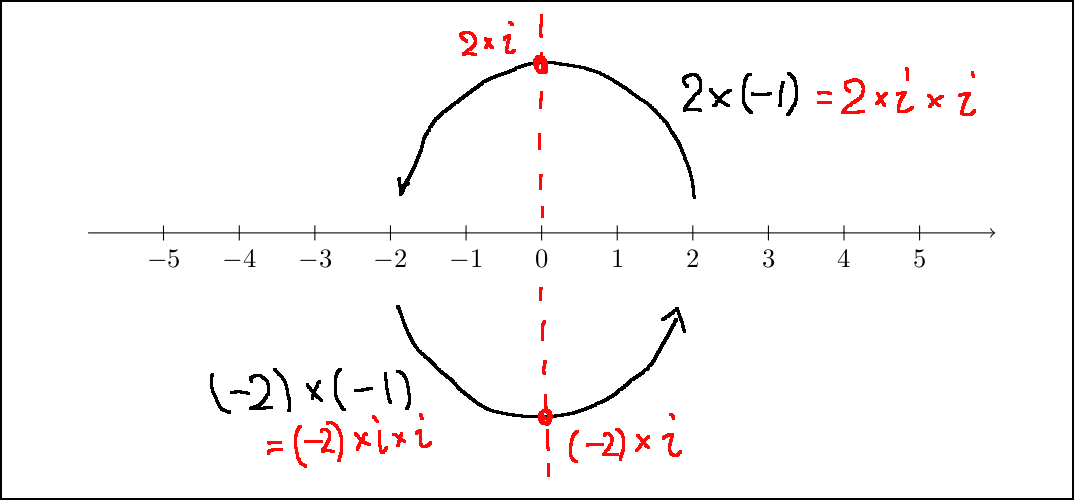
−1をかけると向きが変わるだけで大きさが変わりません。 「2✕(−1)=−2」「(−2)✕(−1)=2」です。 「向きが変わる」というのは「180度回転」させるのと同じです。
ところで、虚数iは2乗すると−1になる数ですから、
2✕(−1)=2✕i✕i
です。では、「2✕i」はどうなるのでしょう? iは2回かけて(−1)で、−1倍は180度の回転でしたから、「i倍は90度回転」と考えればつじつまが合います。
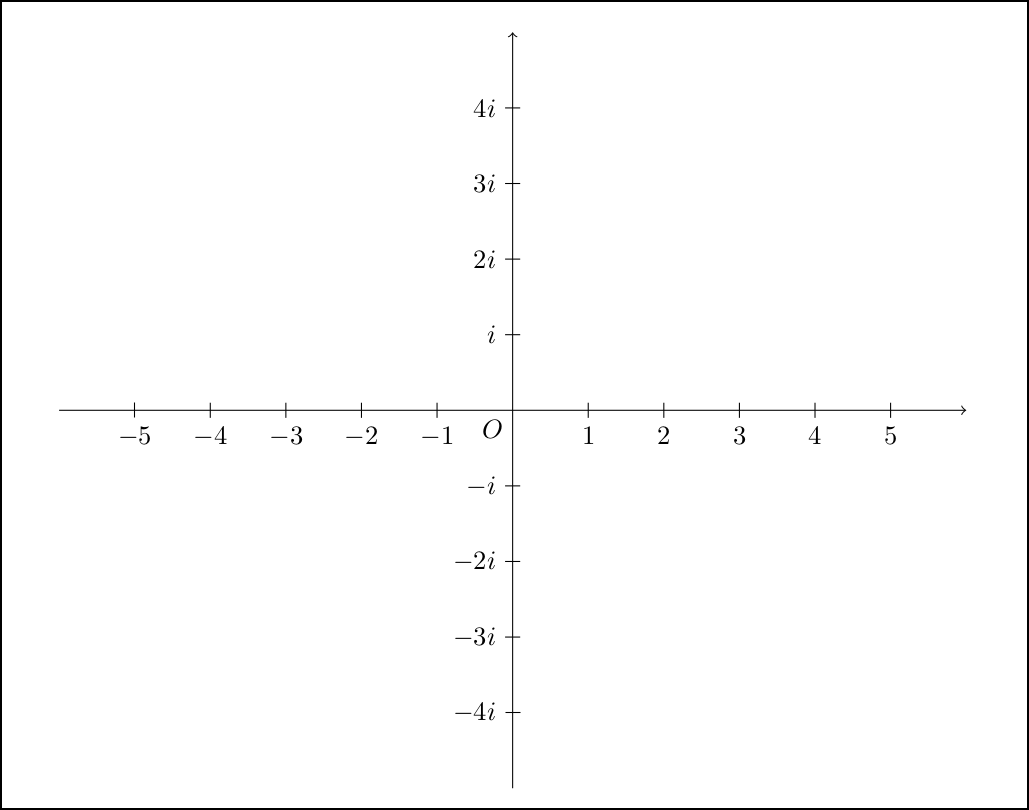
このことから、iの倍数は垂直に並ぶことになります。
これが高校で習う「複素平面」です。 「マイナスをかけると向きが変わる(=180度回転)」を発展させて複素平面の考えにたどり着くわけですね。 もしもマイナス✕マイナスがマイナスだったら、このように発展させることはできませんでした。