パーサ・ジェネレータとは
パーサを日本語で「構文解析器」といいます。 「器」とといっても、「うつわ」ではなく「器械」、より適切にはアプリケーションまたはプログラムのことです。 つまり、構文解析をするプログラムです。
「構文解析」とは、「プログラム言語などの構文」を「解析」することです。 簡単な例として、足し算を考えてみましょう。
1+2 11+34 123+456
3つの足し算の例があります。 出てくる数字は違うものですが、どれも「数字+数字」というパターンは変わりません。 3番めの文字列は7つの文字からなっています。
1, 2, 3, +, 4, 5, 6
この7文字はバラバラではなく、最初の3つがひとまとまりで、「123」という数字を表しており、その後「+」という演算記号、「456」という数字が続きます。 そこで、この7文字をタイプと値のセットで、それぞれ次のようにまとめましょう。
数字, 123 +, 何でも良い 数字, 456
数字には値が必要ですが、演算記号には値がありませんから、2番めの「値」のところは何でも良いのです。
ここでは、同じ演算記号の文字列"+"にしておきましょう。
また、「数字」というタイプは、Numberの最初の3文字をとって、シンボル:NUMで表すことにします。
すると、「123+456」という7文字の文字列は
[[:NUM, 123], ["+", "+"], [:NUM, 456]]
という配列にすることができます。
これを字句解析といいます。
配列の要素の[:NUM,123]を字句またはトークンといいます。
トークンのタイプを表す:NUMなどをタイプとかトークン・カインドといいます。
配列の2番めの要素「123」は値とか、意味上の値(semantic value)などといいます。
字句解析は、構文解析には含まれないというのが一般的な考え方です。
それでは、この構文はどういうものでしょうか。 さきほど述べたように、どの式も「数字+数字」の形です。 そこで、この式(expression)は
expression : NUM '+' NUM
と表すことができます。 式(expression)とは数字(NUM)の次にプラス('+')がきて、その次にまた数字(NUM)がくるというトークンの列のことである、ということです。 この記法をBNF(バッカス・ナウア・フォーム)といいます。
この構文はRaccが理解できる形にしています。
- NUMにはコロンをつけない(:NUMとはしない)
- +はシングルクォートで囲む。
足し算のトークン・カインドを新たに決めることもできますが(例えばPLUSとして、字句解析では[:PLUS, "+"]とする)、演算子はそれ自体をトークン・カインドにすることが多いです。 そのことによって、トークン・カインドの種類が多くなるのを防ぎ、プログラマーの負担を軽くする狙いがあります。 演算子をそのままトークン・カインドにするときは、
とします。シンボルでないことには注意してください。
このように式(expression)を定義すると、最初の3つの足し算はすべてこのBNFに沿っていることがわかります。 このBNFで表されたものを、文法(grammar)といいます。
Rubyなどのプログラム言語はもっと複雑な文法を持っていますが、その文法に入力(ソースファイル)があっているかどうかは確認ができます。 あっていなければ「Syntax Error」(文法上のエラー)となります。
例えば次のような式はさきほどの足し算の文法からはSyntax Errorになります。
1+2+3 10-6 -20
- 「1+2+3」は「1+2」までは文法通りですが、そのあと「+3」があるのでシンタックス・エラー
- 「10-6」は演算子が「+」ではなく「-」なのでシンタックス・エラー
- 「-20」は数字から始まらないのでシンタックス・エラー
この3つはエラーが発見される時点が違います。 最初から順に見ていって、エラーになるところを●で表すと
1+2+●3 10-●6 -●20
黒丸の左側の要素を見た時シンタックスエラーが確定します。
少し複雑な文法
それでは、我々が普段使う足し算、引き算の計算をBNFにしてみましょう。
この計算では、数字、+、ー、(、)の5つのトークンが必要です。 具体例を見てみましょう。
1-2+3 (1-2)+3 1-(2+3)
最初の例は後回しにして、2番めを見てみます。 これは、はじめに1と2の2つの数字を引き算し、その結果と3を加える、というもので、木構造(ツリー)で表現すると
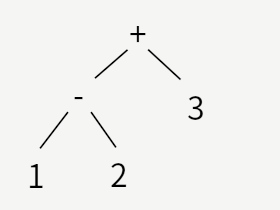
となります。 3番めは同様に、
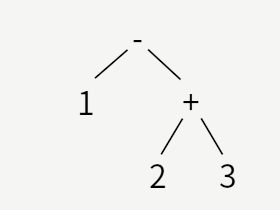
です。
1行目の「1-2+3」には括弧がないので、上の図のどちらのツリーになるか、曖昧さが残ります。
通常は頭から計算するので、1-2を先に計算するのですが、構文解析上はそれを明示する必要があります。
その方法については後ほど述べることにします。
この例では1回の計算の結果が次の式の中で使われています。 つまり、「数字+数字」ではなく「式+式」のような場合があるということです。 そこで、BNFを少し変えてみます。
expression : expression '+' expression | expression '-' expression
縦棒(|)は「または」という意味で、その左側のパターンでも右側のパターンでも良いということです。
このBNFでは、expressionをexpressionで定義しているので、これだけでは構文を表したことになりません。
前は式を「数字+数字」としていました。
少なくとも数字が式の定義に出てこなければいけないでしょう。
そこで、次のように変えてみます。
expression : expression '+' expression
| expression '-' expression
| NUM
このように、定義は2行以上に渡っても良いことにします。 式は「式+式」または「式ー式」または「数字」のいずれかに一致すれば良い、ということです。 これならば、「1-2+3」は式であることがわかります。
- 「
1」は「数字」したがって「式」でもある - 「
1-2」は「式ー数字」だが、数字は式でもあるので、「式ー式」になる。これはBNFの2行目のパターンなので式とみなせる。 - 「
1-2+3」は「1-2」が式なので、「式+3」すなわち「式+数字」だが、数字は式だから「式+式」となり、BNFの1行目のパターンに一致するから式である。
しかし、実は違う方法で式であることも説明できます。
- 「
1-2+3」は「2+3」が「数字+数字」、すなわち「式+式」だから、式となる - 「
1-2+3」は「2+3」が式なので、「数字ー式」となり、数字は式だから「式ー式」となり、BNFの2行目のパターンに一致するから式である。
1−2+3が式であることはBNFで確認できるが、その方法は少なくとも2通りあるということです。 しかも、その計算結果は異なり、それぞれ2と−4になります。 ですから、BNFの解釈が2通りというのはとてもまずいことなのです。 また、この2通りは、さきほど木構造で表した2通りと同じことだとわかります。 ですから、解釈が1通りになるには括弧を加える、というのはひとつの方法です。
expression : expression '+' expression
| expression '-' expression
| '(' expression ')'
| NUM
これだと、「(1−2)+3」や「1−(2+3)」が文法的に合うようになります。 解釈が2通り出てしまう「1−2+3」は防げませんが、そういうものは
- シンタックス・エラーだということにする
- 解釈が2通りでたら「左側の演算から優先的に行う」という条件をつけて1通りに強制する
のどちらかを採用すればよいのです。
また、次のようにBNFを変更すると、常に計算は左から行われるようになります。
expression : expression '+' primary
| expression '-' primary
| primary
primary : '(' expression ')'
| NUM
「1−2+3」がこれでどのように解釈されるか考えてみましょう。 なお、primaryは日本語で一次因子とかプライマリーと呼ばれます。
- 「1−2」は「数字ー数字」で、数字=>プライマリー=>式だから、「式ープライマリー」なので式になる
- 「1−2+3」は「式+3」すなわち「式+数字」になり、それは「式+プライマリー」だから「式」になる
2+3を先に計算する方は上記のBNFには合いません。
- 「2+3」は「数字+数字」=>「式+プライマリー」になるので「式」になる
- 「1−2+3」は「数字ー式」=>「式ー式」になるが、「式ープライマリー」ではない。したがって、式にはならない
このBNFは計算の第二項が「式」ではなく「プライマリー」であるとして、プライマリーが「括弧で囲まれた式」か「数字」のみということで、括弧なしで右から計算することを取り除いています。
以上をまとめると、計算の順序の曖昧さを防ぐ方法は2つあり、
ということになります。
四則(加減乗除)計算のBNF
今回の最後に四則計算の文法定義のBNFを作ってみましょう。 足し算引き算のところで、演算子が2つあったとき、左から計算するか、右から計算するかの2通りの解釈が生まれる場合がありました。 似たものに、乗除と加減の優先順位の問題があります。
1+2*3
ここでは、Rubyと同じように掛け算はアスタリスク(*)で表します。
この計算では、「2かける3」を先にやることになっています。
ですから、
1+2*3 = 1+6 = 7
となります。 これは小学校で習いますね。 ところが、コンピュータはそういうことを習っていませんから、BNFなどで、演算の優先順位を定義しなければなりません。 ところで、「1+6」の1や6を「項(term)」と呼びます。 また、「2*3」の2や3を「因子(factor)」といいます。 BNFだけで演算の優先順位を表現するには式、項、因子を分けて定義します。
expression : expression '+' term
| expression '-' term
| term
term : term '*' factor
| term '/' factor
| factor
factor : '(' expression ')'
| NUMBER
このBNFは「2+3+4」のような括弧のない式は左から順に計算するようになっており、曖昧さが発生しません。 このBNFでは、単項マイナス、すなわち因子の符号を変えるマイナス(例えば「−2」のようなマイナス)はサポートしていません。
Racc で実装
このBNFをRaccのソースファイルに取り入れて、コンパイルしてみましょう。
Raccのソースファイルは拡張子.yにするのが習慣です。
大きく4つのパートに分かれます。
- クラスの定義、BNFの記述部分。この部分はRaccによってRubyプログラムにコンバートされる
- (header)クラス定義の前にコピーされるRubyプログラム
- (inner)クラスの中のコンバートされる部分の前に挿入されるRubyプログラム
- (footer)クラス定義のあとにコピーされるRubyプログラム。メインプログラムを書く場合はここに書く
クラス定義、BNFの記述部分
ここがRaccのソースプログラムのメインです。
スーパークラスは書かないようにします(class A < BのBの部分は書かない)。
tokenの後にトークンを宣言しておく。これは無くても良いが、トークンの綴間違いなどをチェックできる。例えばtoken NUMのようにするoptionsの後にオプションを指定できる。options no_result_varが良く用いられる。その意味はドキュメントを参照rule以降(classのendまで)にBNFを記述する
具体例を次に示します。
class Sample1
token NUMBER
options no_result_var
rule
expression : expression '+' term { val[0] + val[2] }
| expression '-' term { val[0] - val[2] }
| term
term : term '*' factor { val[0] * val[2] }
| term '/' factor { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
| factor
factor : '(' expression ')' { val[1] }
| NUMBER
end
BNFは加減乗除をサポートする以前示したものと同じですが、その後ろに波括弧で囲まれた部分があります。
これはアクションと呼ばれるものです。
アクションの左側のBNFに一致したときに、そのアクションが実行されます。
配列valは左のBNFの要素に対応するアクションが実行されたときの結果です。
例えば
factor : '(' expression ')' { val[1] }
| NUMBER
この2行目にはアクションがありませんが、その場合のアクションは{ val[0] }、すなわち最初のBNFの要素のアクションの結果を返す、ということになっています。
NUMBERは字句解析で返された数字に一致しますので、その値が返されます。
1行目は括弧で囲まれた式です。このBNFには、左括弧、式、右括弧の3つの要素があります。val[1]は2番めの要素である式のアクションの結果です。
したがって、この括弧で囲まれたfactorの値は、括弧で囲まれた式の値になります。
このようにして、それぞれの式に一致したときに、その計算がアクションとして行われます。
なお、定義するクラスをモジュールの中に入れたいときは
class MName::Sample1
のようにします。MNameはクラスを入れるモジュールの名前です。
Raccでコンパイルすると
module MName class Sample1 ... ... ... end end
このようになります。
ヘッダー、インナー、フッター
ヘッダーに良く書かれるのはrequire文です。 このサンプルプログラムでは特に記述するものはありません。
インナーには字句解析関係のプログラムを書きます。
また、Raccで生成したパーサが字句を一つずつ読み込むためのメソッドはnext_tokenというメソッド名に決まっています。
それを実装します。具体例を示します。
def lex(s) @tokens = [] until s.empty? case s[0] when /[+\-*\/()]/ @tokens << [s[0], s[0]] s = s[1..-1] unless s.empty? when /[0-9]/ m = /\A[0-9]+/.match(s) @tokens << [:NUMBER, m[0].to_f] s = m.post_match else raise "Unexpected character." end end end def next_token @tokens.shift end
メソッドlexが引数の文字列を字句解析するプログラムです。
ここでは、StrScanライブラリを使っていませんが、大きなプログラムでは高速な字句解析のためにStrScanを用いるほうが良いです。
その場合は、headerのところにstrscanライブラリをrequireしてください。
演算子は、その文字列をタイプと値にして@tokensにプッシュします。
数字(0以上の整数)はタイプを:NUMにしてその数字(Floatオブジェクトに直したもの)をプッシュします。
IntegerでなくFloatにしたのは、割り算で小数点以下まで出したかったからです。
Integerオブジェクトにしても良いのですが、その場合は割り算で小数点以下は切り捨てられます。
それ以外の文字は例外を発生させます。
メソッドnext_tokenは字句解析の配列からひとつづつ取り出して返します。
フッターの部分にはメインプログラムを書きます。
メインプログラムから、構文解析をするにはdo_parseメソッドをコールします。
そのコールの前にはlexメソッドによる字句解析は終了していなければなりません。
以下の例では一行入力しては、その計算をして表示します。
sample = Sample1.new print "Type q to quit.\n" while true print '> ' $stdout.flush str = $stdin.gets.strip break if /q/i =~ str begin sample.lex(str) print "#{sample.do_parse}\n" rescue => evar m = evar.message m = m[0] == "\n" ? m[1..-1] : m print "#{m}\n" end end
特に難しいことないと思います。 ソースプログラム(sampe1.y)の全体も以下に示しておきます。
class Sample1
token NUMBER
options no_result_var
rule
expression : expression '+' term { val[0] + val[2] }
| expression '-' term { val[0] - val[2] }
| term
term : term '*' factor { val[0] * val[2] }
| term '/' factor { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
| factor
factor : '(' expression ')' { val[1] }
| NUMBER
end
---- header
---- inner
def lex(s)
@tokens = []
until s.empty?
case s[0]
when /[+\-*\/()]/
@tokens << [s[0], s[0]]
s = s[1..-1] unless s.empty?
when /[0-9]/
m = /\A[0-9]+/.match(s)
@tokens << [:NUMBER, m[0].to_f]
s = m.post_match
else
raise "Unexpected character."
end
end
end
def next_token
@tokens.shift
end
---- footer
sample = Sample1.new
print "Type q to quit.\n"
while true
print '> '
$stdout.flush
str = $stdin.gets.strip
break if /q/i =~ str
begin
sample.lex(str)
print "#{sample.do_parse}\n"
rescue => evar
m = evar.message
m = m[0] == "\n" ? m[1..-1] : m
print "#{m}\n"
end
end
コンパイルと実行
コンパイルは「racc ソースファイル名」で行います。
$ racc sample1.y $ ls sample1.y sample1.tab.rb
sample1.tab.rbがRaccで生成されたRubyプログラムです。
このファイルをエディタで見ると、BNFが様々な配列とメソッドに変換されているのがわかります。
実行してみましょう。
$ ruby sample1.tab.rb Type q to quit. > 1-2-5 -6.0 > 2*3+4*5 26.0 > (10+25)/(3+4) 5.0 > q
計算は正しく行われていますね。
演算子の優先順位と結合における左右の優先順位
BNFにあいまいさがあるときに、その解決方法として
- BNFをあいまいさの残らない形に変更する
- 演算の優先順位を指定する
の2つが考えられます。 後者には2つあり、例えば
- 乗除は加減より優先的に計算する。例えば「1+2*3」では「1+2」よりも「2*3」を先に計算する。
このように演算子の間に優先順位をつけることにより、曖昧さを解決できることがあります。
四則では、
- 乗除の優先順位は同じ。つまり「1*2/3」は「1*2」と「2/3」のどちらを先にするかの取り決めはない。この順については別に定めが必要
- 加減の優先順位は同じ。
- 乗除は加減に対して優先順位が高い
- 同レベルの演算があったときに、左から先に計算する(左結合)または右からさきに計算する(右結合)を定める。 通常は加減乗除とも同レベルの演算は左から先に計算する。 右結合は少ないが、無いわけではない。たとえば累乗は右結合である。累乗を「^」で表すと「2^3^4」は「2^81」のことになる。
Raccでは、これらの優先順位を指定することができます。 優先順位をprecedenceといい、Raccはこの最初の4文字を用いて
- prechigh: 優先順位が高い
- preclow: 優先順位が低い
この2つ間に演算子を書き、同じ行には同じ優先順位、上の方が優先順位が高い、とします。
また、左結合はleft、右結合はrightで指定します。
以上のルールを用いると、BNFが単純でもパーサを生成することができます。
Raccのソースファイルの最初の部分を書き換えてみましょう。 なお、footerのインスタンス生成時のクラス名はSample1からSample2に変更が必要です。
class Sample2
token NUMBER
prechigh
left '*' '/'
left '+' '-'
preclow
options no_result_var
rule
expression : expression '+' expression { val[0] + val[2] }
| expression '-' expression { val[0] - val[2] }
| expression '*' expression { val[0] * val[2] }
| expression '/' expression { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
| '(' expression ')' { val[1] }
| NUMBER
end
3行目から6行目が計算順を示す部分です。 このおかげで、BNFは短く、すっきりしたものになりました。
まとめ
この電卓プログラムのソースコードはわずか57行です。 これをRubyで書いたら、そんな短いコードではすみません。
Raccは構文解析が必要なプログラム、例えばインタープリタ、コンパイラ、電卓などを書くときの大きな手助けになります。 言語はCで書かれることが多いですが、Cの場合はパーサ・ジェネレータのBisonを使うことが多いです。 BisonもRaccのようなプログラムです。
Raccを使った電卓プログラムをGitHubにあげてありますので、参考に見てください。
また、Raccのドキュメントはこちらをご覧ください。